1. SIMPLE Algorithm
Governing equations can be written as follows using Rhie-Chow interpolation.
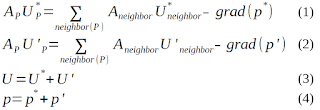
In OpenFOAM, Eq.(1-2) are written as follows.

Step.1:
Solve Eqn.(1') implicitly by p* = p0 (p of previous time) and obtain U*
Step.2:
From continuity equation (div(U) = 0) and Eqn.(3-4), Eqn.(5) can be obtained.

Here, an approximation (Eqn.(6)) was used.

Step.3:
Solve Eqn.(5) implicitly and obtain p.
Step.4:
Correct U using Eqn.(1'-2'), Eqn.(3-4) and Eqn.(6).

Step.5:
Go to next time and repeat from Step.1 if not converged.
2. SIMPLEC Algorithm
In SIMPLEC Algorithm, the following approximation is used instead of Eqn.(6).

In OpenFOAM's expression,

Here we can obtain Eqn.(8) from Eqn.(2'').

Step.1:
Same as SIMPLE Algorithm.
Step.2:
From continuity equation (div(U) = 0), Eqn.(3-4) and Eqn.(8), Eqn.(5') can be obtained.

Step.3:
Solve Eqn.(5') implicitly and obtain p.
Step.4:
Correct U using Eqn.(1'), Eqn.(3-4) and Eqn.(8).

Step.5:
Go to next time and repeat from Step.1 if not converged.
Governing equations can be written as follows using Rhie-Chow interpolation.
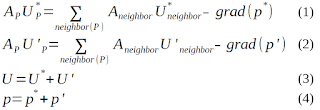
In OpenFOAM, Eq.(1-2) are written as follows.
Step.1:
Solve Eqn.(1') implicitly by p* = p0 (p of previous time) and obtain U*
Step.2:
From continuity equation (div(U) = 0) and Eqn.(3-4), Eqn.(5) can be obtained.

Here, an approximation (Eqn.(6)) was used.
Step.3:
Solve Eqn.(5) implicitly and obtain p.
Step.4:
Correct U using Eqn.(1'-2'), Eqn.(3-4) and Eqn.(6).

Step.5:
Go to next time and repeat from Step.1 if not converged.
2. SIMPLEC Algorithm
In SIMPLEC Algorithm, the following approximation is used instead of Eqn.(6).
In OpenFOAM's expression,

Here we can obtain Eqn.(8) from Eqn.(2'').

Step.1:
Same as SIMPLE Algorithm.
Step.2:
From continuity equation (div(U) = 0), Eqn.(3-4) and Eqn.(8), Eqn.(5') can be obtained.

Step.3:
Solve Eqn.(5') implicitly and obtain p.
Step.4:
Correct U using Eqn.(1'), Eqn.(3-4) and Eqn.(8).

Step.5:
Go to next time and repeat from Step.1 if not converged.
Comments
Post a Comment